Mi e’ tornato in mano un bel libro di Piergiorgio Odifreddi, intitolato C’e’ spazio per tutti che tratta di geometria, e mi ha ispirato alcune riflessioni.
La prima, e’ che benche’ il liceo classico sia intriso di cultura greca, c’e’ una grave mancanza, poiche’ viene insegnata poco la genesi della geometria e della matematica, fortemente connesse nel mondo greco. Cosi’ tanto connesse che gli Elementi di Euclide trattano non solo di Geometria, ma anche di Algebra e Aritmetica.
Il libro di Odifreddi e’ ben fatto per certi versi, ma per altri e’ un po’ una sarabanda di concetti intensi, che meriterebbero piu’ tempo per essere appresi, poiche’ si mischia arte, cultura greca e geometria in un bibitone piu’ simile alla bevanda portentosa di Asterix invece che ha un infuso da bere tranquillamente la domenica mattina. Proviamo quindi a fare qualche osservazione laterale, un po’ piu’ distesa.
C’e’ una osservazione interessante che ho letto su un altro testo, Che cosa e’ la matematica? Introduzione elementare ai suoi concetti e metodi ad opera di Richard Courant, dove nell’introduzione si fa una osservazione cruciale: la scoperta da parte dei greci degli “incommensurabili” li spinse verso la geometria assiomatica, anziche’ verso il calcolo numerico e l’analisi matematica pura.
Gli antichi matematici greci non calcolavano con incognite ed equazioni come noi oggi, usavano invece proporzioni per esprimere le relazioni tra le quantità. Per questo il rapporto tra due quantità simili, non era solo un valore numerale, come pensiamo oggi; il rapporto di due quantità simili era una relazione primitiva tra esse.
Da https://it.wikipedia.org/wiki/Eudosso_di_Cnido#Eudosso_e_la_matematica nella pagina dedicata ad Eudosso
E cosa vuol dire incommensurabile? Non e’ una parolaccia… indica due grandezze che non si possono ridurre ad una medesima unita’.
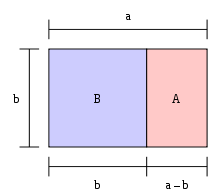
I greci si erano accorti del problema: per esempio nel seguente rettangolo, chiamato rettangolo aureo si nota che c’e’ il seguente rapporto tra i lati:
a:b = b: (a-b)
I lati a e b non sono commensurabili, poiche’ se ponete b=1 viene fuori che a vale un numero irrazionale 1,618… denotato normalmente con la lettera greca ϕche a ache fare con la sezione aurea di cui parleremo tra un attimo
Ma i greci avevano trovato un modo per disegnare questo rettangolo, anche se non potevano mettere in relazione di commensurabilita’ i lati. Al medesimo modo, si accorsero che la diagonale del quadrato era un numero irrazionale, e non tutti la presero bene.
Anche il cerchio conteneva qualche problema, poiche’ il rapporto tra la circonferenza e il diametro era un numero un po’ strano 3,14… ma non disperavano di poterlo esprimere come un rapporto.
La misura di ϕ = 1,618… ha a che fare con la sezione aurea, che fu usata da greci ed egizi in architettura, e poi torno’ in auge durante il nostro Rinascimento.
Si noti che nel rettangolo aureo anche il sotto-rettangolo A e’ aureo e quindi puo’ essere diviso a sua volta nel medesimo modo, e si puo’ andare aventi ricorsivamente sia nell’infinitamente piccolo che all’inverso creando rettangoli sempre piu’ grandi… tutti “belli e proporzionati”. E per i greci una cosa bella (kalos) era anche una cosa buona (agazos)…
Risorse
Per fare stupende animazioni https://docs.manim.community/ e’ un must